14. Text: The Regression Closed Form Solution

How Do We Determine The Line of Best Fit?

You saw in the last video, that in regression we are interested in minimizing the following function:

\sum\limits_{i=1}^n(y_i - \hat{y}_i)^2

It turns out that in order to minimize this function, we have set equations that provide the intercept and slope that should be used.

If you have a set of points like the values in the image here:

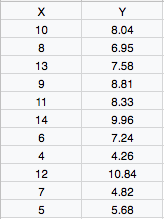
In order to compute the slope and intercept, we need to compute the following:

\bar{x} = \frac{1}{n}\sum x_i

\bar{y} = \frac{1}{n}\sum y_i

s_y = \sqrt{\frac{1}{n-1}\sum\limits(y_i - \bar{y})^2} (Using the Bessell's Correction formula)

s_x = \sqrt{\frac{1}{n-1}\sum\limits(x_i - \bar{x})^2} (Using the Bessell's Correction formula)

r = \frac{\sum\limits_{i=1}^n(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2}\sqrt{\sum(y_i - \bar{y})^2}}

b_1 = r\frac{s_y}{s_x}

b_0 =\bar{y} - b_1\bar{x}

But Before You Get Carried Away…

Though you are now totally capable of carrying out these steps….

In the age of computers, it doesn't really make sense to do this all by hand. Instead, using computers can allow us to focus on interpreting and acting on the output. If you want to see a step by step of this in Excel, you can find that here. With the rest of this lesson, you will get some practice with this in Python.